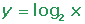FUNCIONES MATEMATICAS
En matemática, una función (f) es una relación entre un conjunto dado X (llamado dominio) y otro conjunto de elementos Y (llamado codominio) de forma que a cada elemento x del dominio le corresponde un único elemento f(x) del codominio (los que forman el recorrido, también llamado rango o ámbito).
1. Funciones algebraicas
En las funciones algebraicas las operaciones que hay que efectuar con la variable independiente son: la adición, sustracción, multiplicación, división, potenciación y radicación.
Las funciones algebraicas pueden ser:
1.1 Funciones polinómicas
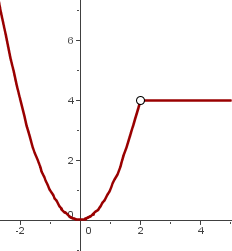
Son funciones definidas por distintos criterios, según los intervalos que se consideren.
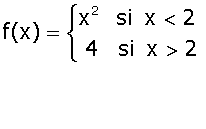
El dominio lo forman todos los números reales menos el 2.
1.2 Funciones racionales
El criterio viene dado por un cociente entre polinomios:
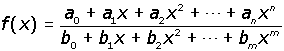
El dominio lo forman todos los números reales excepto los valores de x que anulan el denominador.
Dentro de este tipo tenemos las funciones de proporcionalidad inversa de ecuación:
.
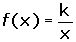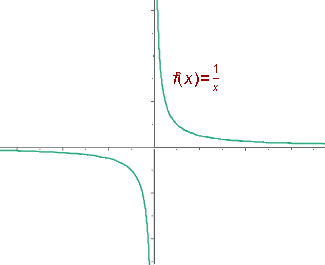
Sus gráficas son hipérbolas. También son hipérbolas las gráficas de las funciones.
1.3 Funciones radicales
El criterio viene dado por la variable x bajo el signo radical.
El dominio de una función irracional de índice impar es R.
El dominio de una función irracional de índice par está formado por todos los valores que hacen que el radicando sea mayor o igual que cero..
Ejemplos
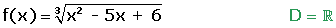
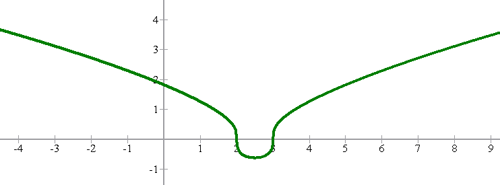
2. Funciones trascendentes
La variable independiente figura como exponente, o como índice de la raíz, o se halla afectada del signo logaritmo o de cualquiera de los signos que emplea la trigonometría.
2.1 Funciones exponenciales
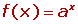
Sea a un número real positivo. La función que a cada número real x le hace corresponder la potencia ax se llama función exponencial de base a y exponente x.
Ejemplos
|
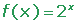
x |
y = 2x |
|
-3 |
1/8 |
|
v-2 |
1/4 |
|
-1 |
1/2 |
|
0 |
1 |
|
1 |
2 |
|
2 |
4 |
|
3 |
8 |
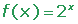
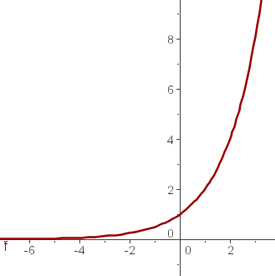
APLICACIÓN
Torre Eiffel (1889)
Esta estructura de hierro pudelado diseñada por Gustave Eiffel aplica el álgebra y el cálculo infinitesimal para desarrollar una ecuación adaptable al peso de la torre. Para hacernos una idea de cómo se aplica, antes se debe comprender qué es una ecuación exponencial.
.2 Funciones logarítmicas
La función logarítmica en base a es la función inversa de la exponencial en base a.
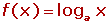
Ejemplos
|
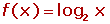
x |
|
|
1/8 |
-3 |
|
1/4 |
-2 |
|
1/2 |
-1 |
|
1 |
0 |
|
2 |
1 |
|
4 |
2 |
|
8 |
2.3 Funciones trigonométricas
1. Función Seno ( Sen):
La Función Seno nos describe la relación existente entre Lado Opuesto sobre la
Hipotenusa. Su simbología es la siguiente:
Función Coseno ( Cos):
La Función Coseno describe la relación entre Lado Adyacente sobre
Hipotenusa. Su simbología es la siguiente:
Función Tangente ( Tan):
Ésta Función nos representa la relación entre Lado Adyacente sobre
Hipotenusa. Su simbología es la siguiente:
También tenemos las Funciones que son inversas a las anteriores:
4. Función Cotangente ( Cot):
Que describe la relación entre Lado Adyacente con Lado Opuesto:
5. Función Secante ( Sec):
Relación entre Hipotenusa sobre Lado Adyacente:
6. Función Cosecante ( CsC):
Nos muestra la relación entre Hipotenusa sobre Lado Opuesto:
