Aplicación de límites en la arquitectura
LIMITES DE FUNCIONES
Se dice que el límite de la función y = f(x), cuando x tiende a p, es igual a L, y escribiremos ,)(límLxfpx=→ sí y sólo sí, dado cualquier ε positivo, siempre es posible encontrar al menos un δ, también positivo y dependiente de él, tal que, si la diferencia de la variable al punto, en valor absoluto, es menor que δ, entonces la diferencia entre los valores de la función en dichos puntos y el límite, en valor absoluto, se mantiene menor que el ε dado.
Ejemplo:
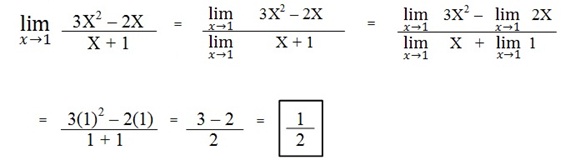
LIMITES UNILATERALES
Definición de límite por la derecha
Se dice que ![]() si y solo si para cada
si y solo si para cada ![]() existe
existe ![]() tal que si
tal que si ![]() entonces
entonces![]() es el límite por la derecha de
es el límite por la derecha de ![]() en "a".
en "a".
Ejemplo:
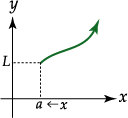
Observe que no hay barras de valor absoluto alrededor de 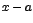 , pues
, pues 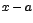 es mayor que cero ya que
es mayor que cero ya que 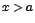 .
.
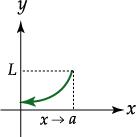
Definición de límite por la izquierda
Se dice que 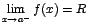 si y solo si para cada
si y solo si para cada 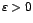 existe
existe 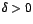 tal que si
tal que si 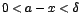 entonces
entonces 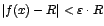 es el límite por la izquierda de
es el límite por la izquierda de 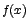 en "a".
en "a".
Ejemplo:
LIMITES INFINITOS
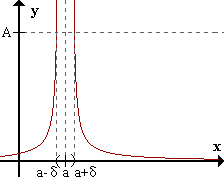
Limx->af(x) = +inf <=> para todo A > 0 existe δ > 0 / para todo x perteneciente al E*a,δ f(x) > A.
El límite de f(x) cuando x->a es infinito positivo, si para cualquier número positivo A (tan grande como se quiera), podemos encontrar un número δ tal que, para todos los x dentro del entorno reducido de a de radio δ se cumple que f(x) es mayor que A.
En otras palabras, si para cualquier número positivo A que consideremos, existe un entorno reducido de a donde la función vale más que A, quiere decir que f(x) puede hacerse mayor que cualquier número, con tal de que x se acerque lo suficiente a a. Por eso se dice que el límite de f(x) cuando x tiende a a es +inf.
Ejemplo:
CONTINUIDAD
Las funciones continuas constituyen la clase básica de funciones para las operaciones del análisis matemático. La idea general de función continua viene a ser la de que su gráfica sea continua; es decir, que la curva pueda dibujarse sin separar el lápiz del papel.
Intuitivamente, la continuidad significa que un pequeño cambio en la variable x implica sólo un pequeño cambio en el valor de f(x), es decir, la gráfica consiste de un sólo trozo de curva.
Vamos a definir la continuidad de una función en un número a.
Definición
Una función f(x) es continua en un punto a si limx->af(x) = f(a).
Nota: observar que debe existir f(a) y debe existir el limx->a f(x) y debe ser igual a f(a).
Ejemplos de discontinuidad

f(x)= 1/x2
Discontinua en x=0 (No existe f(0))

| f(x) = x2 si x <= 2 2x – 4 si x > 2 |
Discontinua en x=2.
Si bien existe f(2), no existe limx->2f(x), pues limx->2-f(x)=4 y limx->2+f(x)=0
Sin embargo, si miramos la función para x próximos a 2 pero menores, e ignoramos los x mayores que 2, la función es continua en 2 “por la izquierda”.
Continuidad por la izquierda
Una función f(x) es continua por la izquierda en el punto a si existe f(a) y limx->a-f(x) = f(a).
Continuidad por la derecha
Una función f(x) es continua por la derecha en el punto a si existe f(a) ylimx->a+f(x) = f(a).
Continuidad en un intervalo (a,b)
- Una función f(x) es continua en un intervalo cerrado [a,b] si:
- f es continua en a por la derecha
- f es continua en b por la izquierda
- f es continua en x, para todo x perteneciente al intervalo abierto (a,b
Clasificación de discontinuidades
Evitable
Caso A:
No existe f(a) pero existe limx->af(x).

f(x)= e-1/x2 + 2
No existe f(0) pues anula un denominador.
limx->0-f(x) = limx->0+f(x) = 2 o sea limx->0f(x)=2
Podemos extender la definición de la función, asignándole en el punto a el valor del límite, con lo cual la función se torna continua. Por ello este tipo de discontinuidad se denomina evitable.
Caso B:
Existe f(a) y existe limx->af(x)=b pero b≠f(a).
(Existe f(a) pero es distinto al valor del límite).
Ejemplo:

f(x) = x2 si x≠2
8 si x=2
f(2) = 8
limx->2 f(x) = 4
Asignándole a la función el valor 4 en x=2, se elimina la discontinuidad.
No evitable
1ª especie:
limx->a-f(x) ≠ limx->a+f(x).
(Los límites laterales son distintos).
Ejemplo:

f(x) = x/(x – 2)
limx->2-f(x) = -inf
limx->2+f(x) = +inf
2ª especie:
No existe limx->a-f(x) o no existe limx->a+f(x).
(No existe por lo menos uno de los límites laterales).
Ejemplo:
